Manuel de géométrie vectorielle/Translations
On a vu, dans le chapitre précédent, qu'un vecteur correspond à un déplacement.
En mathématiques cela correspond à une transformation du plan : la translation.
Définition
D'après le chapitre précédent, on peut énoncer la propriété suivante :
Modèle:Propriété
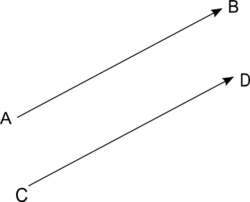
Image d'un point par une translation
On cherche l'image D du point C par la translation de vecteur , c'est-à-dire qu'il faut construire le point D tel que .

Égalité de vecteurs et parallélogrammes
On va maintenant chercher de manière géométrique ce que signifie l'égalité :
- Les vecteurs et ont la même direction : ce qui signifie que les droites et sont parallèles.
- Les vecteurs et ont la même longueur, ce qui signifie que .

On reconnaît là les propriétés d'un parallélogramme.
On en déduit la propriété qui permet de résumer par une égalité vectorielle le fait qu'un quadrilatère soit un parallélogramme. Modèle:Propriété
Construction de l'image d'un point par une translation
Pour placer l'image D du point C par la translation de vecteur , il faut que .
Mais, en utilisant la propriété précédente, si , alors est un parallélogramme.

On peut effectuer la construction du parallélogramme à l'aide d'un compas, comme sur la figure ci-dessous.