Fichier:Savitzky-golay pic gaussien bruite.svg
Aller à la navigation
Aller à la recherche
Taille de cet aperçu PNG pour ce fichier SVG : 610 × 407 pixels. Autres résolutions : 320 × 214 pixels | 640 × 427 pixels | 1 024 × 683 pixels | 1 280 × 854 pixels | 2 560 × 1 708 pixels.
Fichier d’origine (Fichier SVG, nominalement de 610 × 407 pixels, taille : 43 kio)
Description
| Description |
English: Savitzky-Golay algorithm (3rd degree polynomial, 9 points) applied on a gaussian peak with random noise: smoothing (top), first derivation (middle), second derivation (bottom).
The dashed lines highlight the zeros of the second dérivative (inflection points of the peak) and its minimum (top of the peak). Created with Scilab, processed with Inkscape.Français : Application de l'algorithme de Savitzky-Golay sur un pic gaussien bruité (polynôme de degré 3, 9 points) : lissage (haut), dérivée (milieu), dérivée seconde (bas).
Les traits pointillés mettent en évidence l'annulation de la dérivée seconde (points d'inflexion du pic) et son minimum (sommet du pic). Créé avec Scilab, retravaillé avec Inkscape. |
||
| Date | |||
| Source | Travail personnel | ||
| Auteur | Christophe Dang Ngoc Chan | ||
| SVG information | ==Scilab source==
English: English version by default.
Français : Version française, si les préférences de votre compte sont réglées (voir Special:Preferences). | ||
| Code source | (1) Fichier generateur_pic_bruit.sce : crée un nuage de points et l'enregistre dans le fichier pic_gaussien_bruite.txt.
SciLab code// **********
// Constantes et initialisation
// **********
clear;
chdir("monchemin/");
// paramètres de la courbe bruitée
paramgauss(1) = 60; // hauteur de la courbe gaussienne
paramgauss(2) = 3; // largeur de la courbe gaussienne
var=0.01; // variance de la loi normale du bruit
nbpts = 100 // nombre de points
demielargeur = 3*paramgauss(2) // pour intervalle x
pas = 2*demielargeur/nbpts;
// **********
// Fonctions
// **********
// pic gaussien
function [y] = gauss(A, x)
// A(1) : hauteur de pic
// A(2) : "largeur" du pic
y = A(1)*exp(-x.^2/A(2));
endfunction
// **********
// Programme principal
// **********
// Génération des données
for i=1:nbpts
x = pas*i - demielargeur;
X(i) = x;
Y(i) = gauss([paramgauss], x) + rand(var, "normal");
end
// Enregistrement des données
write("pic_gaussien_bruite.txt", [X, Y])
(2) Fichier savitzkygolay.sce : traite les données.
Data// **********
// Constantes et initialisation
// **********
clear;
clf;
chdir("monchemin/")
// paramètres du lissage :
largeur = 9; // largeur de la fenêtre glissante (nb de pts)
degre = 3; // degré du polynôme
// **********
// Fonctions
// **********
// Coefficients de convolution
function [a]=coefconvol(m, d)
// m = largeur de la fenêtre
// d : degré du polynôme
l = (m-1)/2; // demie-largeur de la fenêtre
z = (-l:l)'; // intervalle centré réduit
J = ones(m,d+1);
for i = 2:d+1
J(:,i) = z.^(i-1); // matrice jacobienne
end
A = (J'*J)^(-1)*J';
a = A(1:3,:);
endfunction
// lissage, détermination de la dérivée et de la dérivée seconde
function [y, yprime, yseconde] = savitzkygolay(X, Y, larg, deg)
// X, Y : nuage de points
// larg : largeur de la fenêtre
// deg : degré du polynôme
n = size(X, "*");
l = floor(larg/2);
pas = (X($) - X(1))/(n-1);
// y=Y;
// Ymat = ones(l, n - larg);
// yprime = zeros(Y);
// yseconde = yprime;
a = coefconvol(larg, deg);
a(2, :) = 1/pas*a(2, :);
a(3, :) = 2/pas^2*a(3, :);
for i = 1:larg
Ymat(i, :) = Y(i: n-larg+i)';
end
solution = a*Ymat;
y = solution(1, :)';
yprime = solution(2, :)';
yseconde = solution(3, :)';
endfunction
// **********
// Programme principal
// **********
// lecture des données
donnees = read("pic_gaussien_bruite.txt", -1, 2)
Xinit = donnees(:,1);
Yinit = donnees(:,2);
//subplot(3,1,1)
//plot(Xdef, Ydef, "b")
// Traitement des données
[Yliss, Yprime, Yseconde] = savitzkygolay(Xinit, Yinit, largeur, degre);
// affichage
decal = floor(largeur/2);
nbpts = size(Xinit, "*");
X1 = Xinit((decal+1):(nbpts-decal)); // on enlève les points non lissés
clf;
subplot(3,1,1)
plot(Xinit, Yinit, "b")
plot(X1, Yliss, "r")
subplot(3,1,2)
plot(X1, Yprime, "b")
subplot(3,1,3)
plot(X1, Yseconde, "b")
(3) Si le pas d'échantillonnage n'est pas constant, c'est-à-dire si xi - xi - 1 varie, on peut utiliser une régression linéaire multiple pour déterminer le polynôme. Text// **********
// Constantes et initialisation
// **********
clear;
clf;
chdir("monchemin\")
// paramètres du lissage :
largeur = 9; // largeur de la fenêtre glissante (nb de pts)
// **********
// Fonctions
// **********
// polynôme de degré 3
function [y]=poldegtrois(A, x)
// méthode de Horner
y = ((A(1).*x + A(2)).*x + A(3)).*x + A(4);
endfunction
// régression avec le polynôme de degré 3
function [A]=regression(X, Y)
// X et Y : vecteurs colonne de 9 valeurs ;
// détermine le polynôme de degré 3
// a*x^2 + b*x^2 + c*x + d
// par régression sur (X, Y)
XX = [X.^3; X.^2; X];
[a, b, sigma] = reglin(XX, Y);
A = [a, b];
endfunction
// lissage, détermination de la dérivée et de la dérivée seconde
function [y, yprime, yseconde] = savitzkygolay(X, Y, larg)
// X, Y : nuage de points
// larg : largeur de fenêtre
n = size(X, "*");
decalage = floor(larg/2);
y = Y;
yprime = zeros(Y);
yseconde = yprime;
for i=(decalage+1):(n-decalage)
intervX = X((i-decalage):(i+decalage),1);
intervY = Y((i-decalage):(i+decalage),1);
Aopt = regression(intervX', intervY');
x = X(i);
y(i) = poldegtrois(Aopt,x);
// Yfoo=poldegtrois(Aopt,intervX);
// subplot(3,1,1);plot(intervX, Yfoo, "r")
yprime(i) = (3*Aopt(1)*x + 2*Aopt(2))*x + Aopt(3); // Horner
yseconde(i) = 6*Aopt(1)*x + 2*Aopt(2);
end
endfunction
// **********
// Programme principal
// **********
// lecture des données
donnees = read("pic_gaussien_bruite.txt", -1, 2)
Xinit = donnees(:,1);
Yinit = donnees(:,2);
//subplot(3,1,1)
//plot(Xdef, Ydef, "b")
// Traitement des données
[Yliss, Yprime, Yseconde] = savitzkygolay(Xinit, Yinit, largeur);
// affichage
decal = floor(largeur/2);
nbpts = size(Xinit, "*");
vecteur1 = (decal+1):(nbpts-decal); // suppression des points non-lissés
X1 = Xinit(vecteur1);
Y0 = Yliss(vecteur1);
Y1 = Yprime(vecteur1);
Y2 = Yseconde(vecteur1);
subplot(3,1,1)
plot(Xinit, Yinit, "b")
plot(X1, Y0, "r")
subplot(3,1,2)
plot(X1, Y1, "b")
subplot(3,1,3)
plot(X1, Y2, "b")
|
Conditions d’utilisation
Moi, en tant que détenteur des droits d’auteur sur cette œuvre, je la publie sous les licences suivantes :
|
Vous avez la permission de copier, distribuer et modifier ce document selon les termes de la GNU Free Documentation License version 1.2 ou toute version ultérieure publiée par la Free Software Foundation, sans sections inaltérables, sans texte de première page de couverture et sans texte de dernière page de couverture. Un exemplaire de la licence est inclus dans la section intitulée GNU Free Documentation License. |
Ce fichier est sous licence Creative Commons Attribution – Partage dans les Mêmes Conditions 3.0 Non Transposé, 2.5 Générique, 2.0 Générique et 1.0 Générique.
- Vous êtes libre :
- de partager – de copier, distribuer et transmettre cette œuvre
- d’adapter – de modifier cette œuvre
- Sous les conditions suivantes :
- paternité – Vous devez donner les informations appropriées concernant l'auteur, fournir un lien vers la licence et indiquer si des modifications ont été faites. Vous pouvez faire cela par tout moyen raisonnable, mais en aucune façon suggérant que l’auteur vous soutient ou approuve l’utilisation que vous en faites.
- partage à l’identique – Si vous modifiez, transformez ou vous basez sur cet élément, vous devez distribuer votre contribution sous une license identique ou compatible à celle de l’original.
Vous pouvez choisir l’une de ces licences.
Historique du fichier
Cliquer sur une date et heure pour voir le fichier tel qu'il était à ce moment-là.
| Date et heure | Vignette | Dimensions | Utilisateur | Commentaire | |
|---|---|---|---|---|---|
| actuel | 9 novembre 2012 à 14:07 | 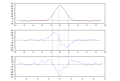| 610 × 407 (43 kio) | wikimediacommons>Cdang | dashed line to highlight the inimum of the second derivative |
Utilisation du fichier
Les 2 pages suivantes utilisent ce fichier :
