Hydrodynamique des fluides parfaits

Débits

Débit volumique

Si pendant un temps $\mathrm{\Delta }t$ il passe un volume $\mathrm{\Delta }V$ alors le débit volumique $Q_V$ est donné par $Q_V=\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}$

Sur le schéma suivant,

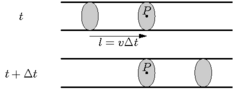
on s'intéresse au volume $V$, compris entre les deux sections grisées, qui passe au point $P$ entre les instants $t$ et $t+\mathrm{\Delta }t$. À ce point la vitesse du fluide est $v$. Donc, la longueur du volume est donnée par $l=v\mathrm{\Delta }t$. Donc $V=Sv\mathrm{\Delta }t$, avec $S$ la section de l'écoulement, on a $Q_V=\frac{Sv\mathrm{\Delta }t}{\mathrm{\Delta }t}=Sv$

Pour un fluide incompressible, le volume se conserve tout le long d'un écoulement. Donc, en tout point de l'écoulement, il passe le même volume $\mathrm{\Delta }V$ dans le même temps $\mathrm{\Delta }t$. Il y a donc conservation du débit volumique. C'est à dire, qu'en tous points $A$ et $B$ d'un écoulement on a $Q_{V,A}=Q_{V,B}=Q_{V,C}$

Débit massique

Si pendant un temps $\mathrm{\Delta }t$ il passe une masse $\mathrm{\Delta }m$ alors le débit massique $D_m$ (ou $q_m$) et donné par $D_m=\frac{\mathrm{\Delta }m}{\mathrm{\Delta }t}$

On peut relier le débit massique au débit volumique. En effet, on a $\mathrm{\Delta }m=\rho \mathrm{\Delta }V$ donc $D_m=\frac{\rho \mathrm{\Delta }V}{\mathrm{\Delta }t}$

De même, en utilisant l'équation eq:dv2 on obtient $D_m=\rho Sv$

Pour un fluide incompressible, on obtient la même propriété sur les débits massiques que sur les débits volumiques. C'est à dire qu'en tous points $A$ et $B$ de l'écoulement on a $D_{m,A}=D_{m,B}$

Propriétés

Variation de la vitesse en fonction de la section

Soit une portion d'écoulement d'un fluide incompressible

D'après la conservation des débits on a $D_{V,A}=D_{V,B}\Rightarrow S_A{v}_A=S_B{v}_B\Rightarrow v_A=\frac{S_B}{S_A}{v}_B$

Comme $S_A>S_B$ alors $V_A<v_B$. Ce qui est intuitif. Pour faire passer le même débit par une section plus petite, il faut que la vitesse augmente.

On retiendra que plus la section d'un écoulement se resserre, plus la vitesse augmente.

Loi des nœuds hydrauliques

Soit la situation suivante :

Pour un fluide incompressible, on a : $D_{V,1}+D_{V,2}=D_{V,3}+D_{V,4}$.

On peut généraliser ce résultat : À un nœud hydraulique, la somme des débits entrants (volumique ou massique) est égale à la somme des débits sortants.

L'équation de Bernoulli

Écoulement et ligne de courant

Attention, un écoulement permanent (dont les vitesses sont constantes) n'est pas un écoulement uniforme (toutes les vitesses sont égales)!

Pour un écoulement uniforme, les lignes de courant représentent la trajectoire qu'aurait une petite particule plongée dans l'écoulement.

L'équation de Bernoulli

Pour un écoulement permanent d'un fluide incompressible on a, entre deux points $A$ et $B$ d'une même ligne de courant: $P_B+\rho g{z}_B+\frac{1}{2}\rho v_B^2-(P_A+\rho g{z}_A+\frac{1}{2}\rho v_A^2)=\frac{{𝒫}_{\mathrm{e}\mathrm{x}\mathrm{t}}}{D_V}$

Avec

 * $P_B$ la pression au point $B$
 * $\rho$ la masse volumique du fluide
 * $g=10\mathrm{m}.{\mathrm{s}}^{-2}$ l'accélération de la gravitation
 * $z_B$ l'altitude du point $B$
 * $v_B$ la vitesse du point $B$
 * ${𝒫}_{\mathrm{e}\mathrm{x}\mathrm{t}}$ la puissance des actionneurs extérieurs (pompe,
   turbine,…). 
   Si l'actionneur fourni de la puissance (pompe,…) alors ${𝒫}_{\mathrm{e}\mathrm{x}\mathrm{t}}>0$.
   Si l'actionneur reçoit de la puissance (turbine,…) alors ${𝒫}_{\mathrm{e}\mathrm{x}\mathrm{t}}<0$.
 * $D_V$ le débit volumique 

Remarque: dans tous les exercices les conditions d'application du théorème de Bernoulli seront réunies.

Applications

Limite hydrostatique

Dans le cas hydrostatique, les vitesses sont nulles ($v_A=v_B=O$) et il n'y a pas d'actionneur extérieur ($𝒫=0$) donc d'après la formule de Bernoulli donnée ci-dessus on a $P_A+\rho g{z}_A=P_B+\rho g{z}_B$

On retrouve alors la relation fondamentale de la statique des fluides (qui n'est donc qu'un cas particulier du théorème de Bernoulli).

Vidange d'un réservoir --- Formule de Torricelli

On réalise la vidange d'un réservoir par un robinet situé au fond de celui ci. On place le point $A$ ($P_A=P_{\mathrm{a}\mathrm{t}\mathrm{m}\mathrm{o}}$) au niveau de la surface libre du réservoir et le point $B$ à la surface du jet sortant du robinet ($P_B=P_{\mathrm{a}\mathrm{t}\mathrm{m}\mathrm{o}}$). On prend comme référence des altitudes le fond du réservoir (donc $z_B=0$ et $z_A=h$). Il n'y a pas d'actionneur entre les points $A$ et $B$ (${𝒫}_{\mathrm{e}\mathrm{x}\mathrm{t}}=0$).

L'équation de Bernouilli (→) devient alors $P_{\mathrm{a}\mathrm{t}\mathrm{m}\mathrm{o}}+\rho gh+\frac{1}{2}\rho v_A^2=P_{\mathrm{a}\mathrm{t}\mathrm{m}\mathrm{o}}+\frac{1}{2}\rho v_B^2$

Le fluide étant incompressible il y a conservation du débit volumique entre les points $A$ et $B$. Soit $D_{V,A}=D_{V,B}\Rightarrow S_A{v}_A=S_B{v}_B\Rightarrow v_A=\frac{S_B}{S_A}{v}_B$

Or, la section $S_A$ au point $A$ est (en général) très supérieure à la section du robinet ($S_B$). Si $S_A\gg S_B\Rightarrow \frac{S_B}{S_A}\ll 1\Rightarrow v_B\gg v_A\Rightarrow v_A^2\ll v_B^2$. On peut alors négliger le terme en $v_A^2$ dans l'équation eq:tori1.

On a alors, après simplification par $P_{\mathrm{a}\mathrm{t}\mathrm{m}\mathrm{o}}$ et réorganisation $v_B=\sqrt{2gh}$

Cette équation n'est pas à savoir (comme toutes les équations de cette partie) mais il faut connaître la démonstration et les hypothèses qui permettent de la retrouver.

Dimensionnement d'une pompe

On cherche à dimensionner la pompe $P$ pour amener de l'eau d'un réservoir jusqu'à une altitude $h$

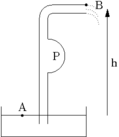
Comme pour la section précédente, on a $P_A=P_B=P_{\mathrm{a}\mathrm{t}\mathrm{m}\mathrm{o}}$, $z_A=0$ et $z_B=h$. On peut généralement faire la même approximation sur les sections du fluide en $A$ et en $B$, donc on peut négliger $v_A^2$. La formule de Bernoulli (→) devient alors (après simplification des pressions) $\rho gh+\frac{1}{2}\rho v_B^2=\frac{{𝒫}_{\mathrm{e}\mathrm{x}\mathrm{t}}}{D_V}$

Il est possible de réécrire cette équation en fonction du débit massique $D_m=\rho S{v}_B$. On a alors ${𝒫}_{\mathrm{e}\mathrm{x}\mathrm{t}}=D_m(gh+\frac{1}{2}\frac{D_m^2}{{\rho }^2{S}^2})$

Effet Venturi

Soit un écoulement possédant un resserrement

Dans l'équation de Bernoulli (→), on a des altitudes égales ($z_A=z_B$) et aucun actionneur (${𝒫}_{\mathrm{e}\mathrm{x}\mathrm{t}}=0$). On obtient donc $P_A+\frac{1}{2}\rho v_A^2=P_B+\frac{1}{2}\rho v_B^2\Rightarrow P_A-P_B=\frac{1}{2}\rho (v_B^2-v_A^2)$

En utilisant l'équation de conservation du débit, on obtient $P_A-P_B=\frac{1}{2}\rho v_B^2(1-\frac{S_B^2}{S_A^2})$

Comme $S_B<S_A$ on a $P_A-P_B>0$ soit $P_B<P_A$. On voit donc que plus l'écoulement se rétrécit, plus la pression diminue.

Ce résultat contre-intuitif est aussi appelé ``paradoxe de Venturi. Cet effet est pourtant bien réel, c'est notamment lui qui est responsable de l'arrachement des toits des maisons lors des tempêtes, ou bien encore c'est le principe du vol des avions.